Les avalanches sont des écoulements rapides de neige sur des pentes de montagne. La plupart des avalanches se déplacent sur quelques centaines de mètres à une vitesse relativement faible (quelques mètres par seconde), mais certaines peuvent se déplacer sur plusieurs kilomètres et d’autres ont été observées avec des vitesses dépassant les 360 km/h. Les avalanches peuvent également générer des forces considérables et pulvériser des structures en acier ou en béton armé. Leur hauteur ne dépasse généralement pas quelques mètres, mais certaines avalanches atteignent des vitesses telles qu’un entraînement massif d’air ambiant se produit, ce qui conduit à la formation de grands nuages de neige, avec des hauteurs dépassant 100 m.
Comme elles mobilisent de la neige sur une pente, les avalanches sont une menace typique des zones de montagne, partout où il existe un couvert neigeux saisonnier ou permanent. A l’échelle mondiale, le nombre de morts et les dommages aux infrastructures causés par les avalanches sont bien moindres que pour les autres dangers naturels tels que les inondations et les tremblements de terre. Pourtant, l’importance économique des activités (par exemple, l’exploitation minière, la production d’électricité, le tourisme) et des axes de communication à travers les massifs montagneux a motivé l’étude de la dynamique des avalanches et le développement de techniques de protection paravalanche. La nivologie (science de la neige et des avalanches) s’est développée au même rythme que les activités humaines en montagne. Son histoire est vieille de plusieurs siècles. Elle a d’abord concerné quelques pays dans le monde (Suisse, France, Autriche, Russie), qui sont encore parmi les principaux acteurs. Puis, au cours des dernières décennies, d’autres pays (Italie, États-Unis, Canada, Japon, Islande, Norvège, Inde, etc.) ont joué un rôle croissant dans le développement de nouvelles techniques et connaissances en nivologie.
Des modèles dès les années 1920
À ma connaissance le premier modèle d’avalanche est dû à un ingénieur RTM, Paul Mougin, en 1922. Ce modèle a été appliqué notamment (par Henri Lagotala, un ingénieur suisse déjà !) pour le téléphérique du Plan de l’Aiguille, construit pour les Jeux Olympiques de 1924 et endommagé juste après. Il y a eu par la suite beaucoup de variantes dans différents pays (principalement Suisse, Japon, URSS, États-Unis, et dans une moindre mesure Autriche et Italie), dont la plus connue est celle de Voellmy (1955).
La seconde génération de modèles est due à Bruno Salm en 1966. C’est la base de tous les modèles de calcul actuels. Pour des raisons évidentes de moyens de calcul, Salm a été obligé d’avoir une version très simplifiée de l’équation du mouvement, qui puisse se résoudre analytiquement. En parallèle à la recherche orientée vers la pratique du SLF (modèle suivi par les Autrichiens, les Canadiens, et les Américains), il y a eu deux autres écoles plus académiques qui se sont concentrées sur la résolution numérique des équations du mouvement :
l’école soviétique (Grigorian, Eglit, etc.) qui s’est intéressée à des modèles hydrauliques dès 1967 et a produit plusieurs modèles de grand intérêt. Il faut aussi signaler, sans entrer dans la polémique, que malgré le Rideau de fer, certains Occidentaux avaient connaissance de ces travaux et les ont plagiés sans état d’âme ;
l’école française, qui sous l’impulsion de Gérard Brugnot et Rémi Pochat dès la fin des années 1970 développent des modèles hydrauliques d’avalanche. La question de leur résolution numérique a été abordée par Jean-Paul Vila. dont on peut considérer qu’il est le père des modèles hydrauliques numériques d’avalanches. Il a donc influencé la génération suivante (Mohamed Naaim, André Paquier pour le Cemagref), mais plus globalement la communauté des mathématiciens appliqués français (avec Pascal Noble, Didier Bresch, etc.). Signalons que les modèles numériques bidimensionnels – sur la base du schéma de Vila – existaient déjà au Cemagref dès le début des années 1990, notamment avec la thèse de Gilbert Martinet. les travaux de Mohamed Naaim et les miens. Je ne suis pas exhaustif. Il me faudrait citer Béghin, Hopfinger, Tochon-Danguy, Carry, etc.
En parallèle des modèles scientifiques de dynamique des avalanches, se sont développées des approches simplifiées pour répondre aux besoins des praticiens dès les années 1970. Là encore on trouve une littérature abondante, avec des pères fondateurs (les Suisses Bruno Salm, André Roch, Hans Frutiger, etc, mais également les Américains comme Ted LaChapelle et Ron Perla), mais aussi des travaux plus diffus dans la littérature universitaire. On peut se rapporter au manuel de la FAO de 1978. Je crois aussi que l’état d’esprit suisse préfère l’orientation vers un cadre global de calcul qui permette de répondre aux différents cas de figure surtout si l’outil est dès son origine orienté vers la pratique. L’approche de Salm a évolué au fil du temps, se consolidant lentement grâce à plusieurs collaborateurs du SLF jusqu’en 1990.
L’approche intégrée des directives suisses
L’apport principal des Suisses pour répondre aux praticiens a été de fournir une approche globale d’estimation du risque d’avalanche. On y retrouve les pères fondateurs Salm et ses collègues du SLF, mais le projet aboutit surtout avec le travail d’André Burkard et celui de Hans Gubler, qui mettent tous les morceaux du puzzle en place et testent la méthode sur des cas concrets documentés. Le point phare a été la publication des « directives suisses » en 1990. La traduction a rendu le texte disponible dès 1992 pour l’espace francophone. Il faut apporter une attention particulière à ce que les Suisses appellent « directives ». Ce ne sont pas des textes réglementaires contrairement à ce qui est souvent considéré en France, mais des guides techniques, des aides à la décision, etc. « Anleitung » renvoie à l’idée d’instructions, de méthodes, de « tutoriel » pour prendre le terme anglais.
Ces modèles simples ont été d’un usage courant parmi tous les praticiens en Europe dès les années 1980. Ils ont été complétés par d’autres outils. Par exemple,
François Rapin (Cemagref) a proposé une version numérique d’aérosol AVAER (de Pierre Béghin) dès les années 1990. Gilles Borrel présentait en 1990 la procédure suivie au Cemagref où la délimitation des zones faisait appel à des critères quantitatifs voisins de ceux employés en Suisse.
D’autres approches
Parallèlement aux modèles de dynamique (où l’on se sert des lois de la physique pour déduire des informations sur les avalanches), il existe aussi des modèles statistiques d’avalanches, qui sont quasiment aussi vieux que les modèles dynamiques. Les Américains de l’USDA Forest Service les employaient dans les années 1970. Ces modèles ont connu leur heure de gloire avec les Norvégiens, mais les Français n’ont pas été en reste, avec notamment la thèse de Ghali Adjel en 1996 au Cemagref, les travaux de Maurice Meunier, et plus récemment tout le travail de Nicolas Eckert.
Progresse-t-on ?
Si on compare un vieux manuel sur les avalanches (comme le manuel de la FAO de 1978) avec les ouvrages actuels, force est de constater que l’évolution des connaissances pratiques est très lente. Très peu de progrès de grande ampleur ont été accomplis en 30 ans, mais on a beaucoup plus d’informations, qui permettent d’affiner, en principe, nos connaissances. Mais contrairement à un lieu commun, ce n’est pas parce qu’on a plus d’informations que l’on s’approche de la vérité physique… La fiabilité des modèles ne vaut que parce qu’il y a un choix pertinent des paramètres du modèle et du type de modèle. D’où l’importance du calage et de l’information a priori qui alimente le modèle.
L’accroissement de la puissance des ordinateurs individuels et l’existence d’interface graphique (GUI) ont facilité considérablement la mise en œuvre des outils numériques. Si l’on considère une loi empirique comme la loi de Moore (le doublement périodique de la puissance tous les 18 mois), on a une variation en loi puissance de la puissance des ordinateurs. Cette loi empirique connaît des contraintes physiques (finesse de gravure des processeurs, nombre de processeurs, puissance électrique, etc.). Pour faire tourner un modèle 2D, il fallait beaucoup d’heures en 1992 sur une station de calcul dédiée de type Appolo ou Sun alors qu’en 2013 cela se fait avec un PC et un bon processeur core i5 ou i7. Cela veut juste dire qu’il est plus facile de faire des calculs, cela ne garantit en rien que les modèles soient plus performants.
Le cœur des modèles n’a guère évolué depuis 20 ans, notre compréhension physique progresse lentement et pas de manière linéaire. Un bon praticien, avec une bonne expérience de terrain et/ou un excellent sens physique, sait tirer profit d’un modèle numérique. Le modèle permet des éclairages nouveaux, il peut aider à construire le raisonnement. Par exemple, si on connaît une distance d’arrêt d’une avalanche historique, on peut caler un coefficient de frottement et voir ce que le modèle dit pour les vitesses de l’écoulement. La condition sine qua non de l’utilisation d’un modèle doit être une solide connaissance des phénomènes de la part du praticien. Notamment ce dernier doit être capable de se forger une première idée sans modèle. Le modèle n’est pas un substitut, n’est pas une béquille, c’est un complément. André Burkard (1992) est encore plus explicite :
« les cartes de danger d’avalanche (CDA) ne doivent être élaborées que par des praticiens reconnus. Les connaissances pratiques nécessaires ne peuvent être obtenues que par la capacité d’observation, l’expérience (que chacun doit acquérir par lui-même), un bagage suffisant dans l’art des avalanches et des techniques de protection. En ce qui concerne le calcul technique des avalanches, il faut garder à l’esprit qu’aucune avalanche est strictement calculable et que chaque avalanche nécessite un traitement particulier. Pour cette raison, il n’existe pas de recettes pour élaborer ou éventuellement ajuster des CDA. De ce fait, l’élaboration des CDA ne provoque jamais l’ennui ! »
Des défis à relever
Une des difficultés rencontrées par les modèles actuels est l’absence de connaissance de la rhéologie de la neige. Aujourd’hui, par usage et par défaut, on emploie une loi empirique scalaire (c.-à-d. ici, une seule variable d’espace, la direction d’écoulement est considérée), qui est la loi de Voellmy. Cette loi fait appel à deux coefficients de frottement (ξ et μ), qui ne sont pas des grandeurs physiques. On ne peut pas les mesurer à partir d’un échantillon de neige prélevé in situ. Il faut les caler à partir de données de terrain. Comme pendant longtemps la seule donnée facilement disponible a été la distance d’arrêt, on les a calés sur des distances d’arrêt. Naturellement, s’il y a deux inconnues, il nous faudrait deux conditions pour que le système d’équations soit fermé. Ce sont des considérations de vitesse et de pression d’impact qui ont servi à fermer les équations. Parfois, on a pu mesurer la vitesse de l’écoulement et donc directement ajuster le second coefficient. Sur le site du Lautaret, le calage des coefficients du modèle de Voellmy donne des valeurs très différentes de celles retenues par les Suisses dans le modèle VSG, notamment les valeurs de ξ sont bien plus élevées. Remarquant que le modèle de Coulomb (c.-à-d. un modèle de Voellmy avec ξ→∞) décrivait bien l’évolution de la vitesse d’une avalanche. j’ai tenté de faire des calages sur les distances d’arrêt pour obtenir des statistiques sur le coefficient de frottement μ. Les analyses sur plusieurs couloirs d’avalanche montrent qu’il n’y a pas de distribution universelle de ce paramètre. La conclusion est que contrairement aux fluides newtoniens, nous avons une loi empirique (pour un site donné) qui décrit approximativement les vitesses observées et/ou les distances d’arrêt pour certains types d’avalanche (et donc pas toutes les formes connues d’avalanche), mais les paramètres sont conceptuels, ils n’ont aucune réalité physique intrinsèque (ils amalgament une multitude de processus physiques). Selon le modèle et le mode de résolution, on obtient des valeurs de calage différentes. Ainsi, si on compare des modèles numériques de type Saint-Venant avec frottement de Voellmy, qui sont censés résoudre les mêmes équations du mouvement, mais peuvent différer dans leur mise en œuvre, on obtient des valeurs bien différentes (voir la comparaison faite par Barbolini et ses collègues). De même, si on cale un jeu de coefficients avec un modèle 1D sur un événement donné, le calage avec un modèle 2D donnera des valeurs différentes. En bref, le problème du choix des paramètres de frottement reste entier et au final, la sélection d’un jeu de paramètres est de la seule responsabilité du chargé d’étude. Comment varient ces paramètres d’un couloir à l’autre sur un même site ou comment ils varient en fonction de la période de retour sont également des questions ouvertes.

Diversité de la neige mobilisée par les avalanches. Clichés Christophe Ancey. (a) neige humide en bloc, (b) neige sèche avec faible teneur en eau liquide (boules friables), (c) neige compactée en boules dures et glacées, (d) plaque de neige frittée.
Outre ce problème de rhéologie non connue de la neige, il y a une multitude de problèmes tout aussi complexes qui sont encore moins connus. Le passage d’une rhéologie 1D à une rhéologie 2D/3D est un problème ouvert. En l’état actuel de nos connaissances et de ce que nous sommes capables de vérifier expérimentalement, le degré de spéculation apparaît comme très élevé. Il faut ensuite évoquer le problème de la structuration des écoulements (formation de bourrelets, ségrégation de boules), le couplage thermodynamique/ thermomécanique (compression de la neige, apparition d’eau liquide favorisant la formation de boules de neige), la topographie (établie l’été, mais plus ou moins différente l’hiver selon l’enneigement), l’entraînement de neige et la déposition, les sur-avalanches (problème considéré comme majeur par le SLF en février 1999 ), le couplage entre un écoulement dense et une partie en aérosol… Tout cela constitue les thèmes de la recherche actuelle. Aujourd’hui, à supposer que l’on connaisse le comportement rhéologique, personne ne sait calculer le comportement d’une masse finie de matériaux sur une topographie quelconque. A fortiori, pour un matériau aussi compliqué que la neige, les modèles actuels simplifient considérablement la problématique. Pour autant, beaucoup (dont moi) s’accordent à dire qu’on arrive à capturer une partie de la physique, mais on est loin d’avoir un outil opérationnel. On tombe là sur un problème similaire avec ce qui se passe sur les modèles climatologiques, qui donnent des tendances, mais les résultats sont contradictoires d’un modèle à l’autre et leur précision est faible, d’autant plus qu’on cherche à extrapoler sur des horizons lointains. Comme le disait un ingénieur valaisan :
« quelle que soit la topographie, un modèle numérique arrivera toujours à montrer que le matériau s’écoule vers le bas… Tous les modèles, même les plus mauvais, arrêteront l’écoulement lorsque celui-ci arrive contre un mur. Reste à savoir ce qui se passe pour l’étalement latéral… »

Avalanche de l’Arcelle, mai 1983. Débordement du lit torrentiel et formation de plusieurs langues au cheminement complexe sur le cône de déjection. Dans ce cas précis, la topographie n’est pas le facteur explication ; c’est la succession des différentes « vagues » de neige, qui crée des points de blocage et de débordement. La formation de bourrelets latéraux (ségrégation latérale des boules de neige) évite l’étalement de l’avalanche, lui permettant ainsi d’aller relativement bas. Source : DR.

Détail de l’avalanche de la combe du Pra, avril 2000. Cliché Toraval. La formation de boules et de gros blocs sans cisaillement (glissement basal pur), l’érosion et l’auto-chenalisation de l’écoulement sont des processus complexes que l’on ne comprend pas. La dynamique d’ensemble est commandée par une faible teneur en eau, qui conditionne l’apparition d’un film d’eau liquide permettant la lubrification, donc le glissement des blocs, ainsi que la cohésion de volumes massifs de neige. Source : Toraval.
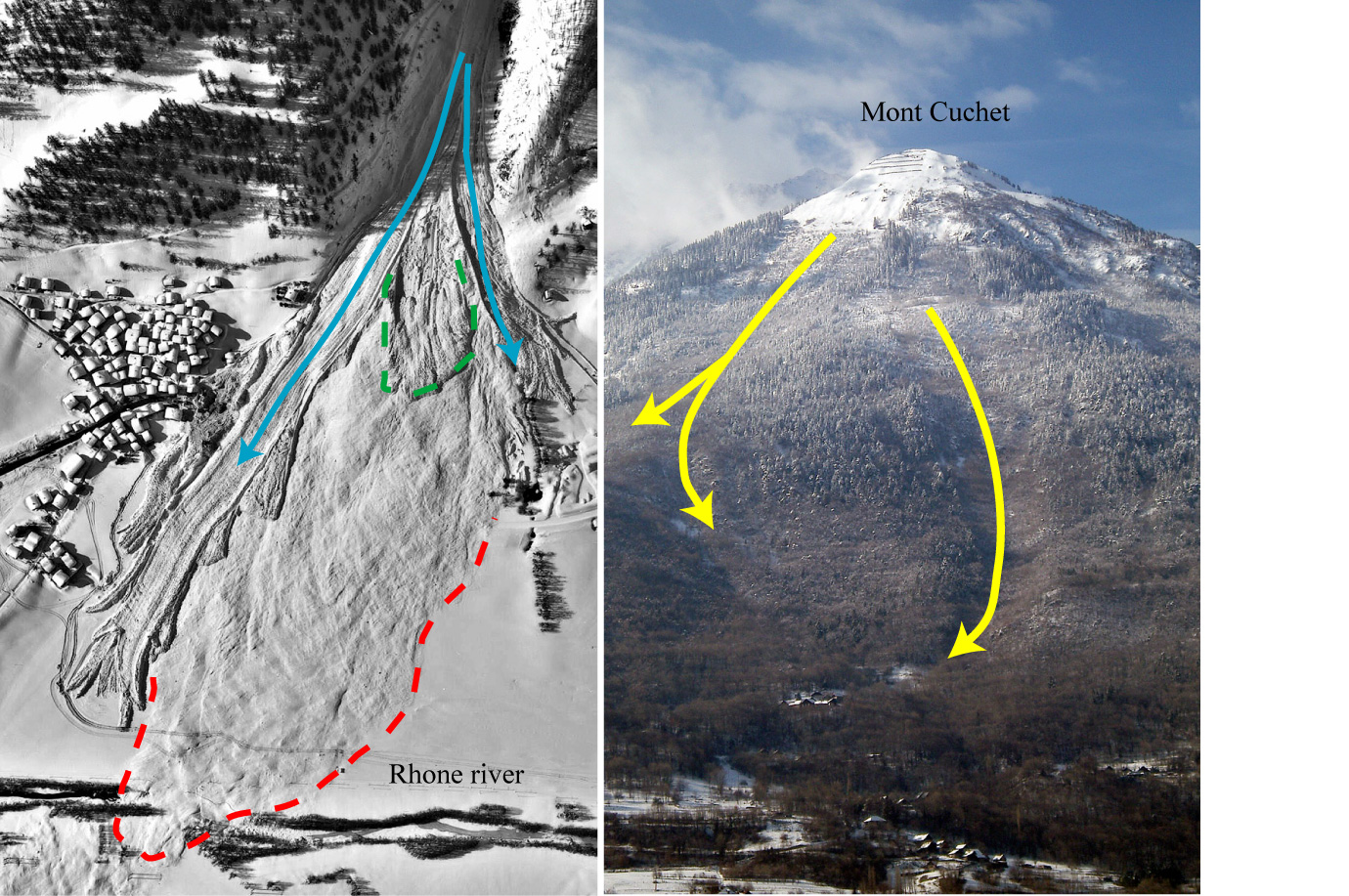
À gauche, avalanches de Geschinen (vallée de Conches, Suisse), février 1999. Cliché Bundesamt für Topographie (SwissTopo). Certaines avalanches forment des dépôts, dont l’extension est difficilement prévisible. C’est le cas par exemple lorsque plusieurs avalanches se produisent et modifient la topographie locale, par exemple en remplissant le lit d’un torrent ou le volume de stockage d’une digue paravalanche. Un exemple est donné par l’avalanche du 23 février 1999 à Geschinen. En deux jours, trois avalanches de grande ampleur se sont produites. La première avalanche fut vraisemblablement un puissant aérosol, qui atteignit le Rhône. Dans sa zone de départ, l’avalanche vida également un lac naturel, dont les eaux contribuèrent à fortement humidifier le manteau neigeux composé de neige sèche et froide. Les deux avalanches suivantes mobilisèrent de la neige humide. Le dépôt épais et massif de la seconde avalanche agit comme une étrave en scindant la troisième avalanche en deux branches, dont l’une vint buter contre la digue haute d’environ 7 m protégeant Geschinen. Cette digue se révéla insuffisante à contenir plusieurs langues d’avalanche. À droite, vue du mont Cuchet en Maurienne. Le hameau du Tremble à Saint-Étienne-de-Cuines (Savoie) a été touché en janvier 1981 par des avalanches issues du mont Cuchet malgré l’importante forêt. Cliché Toraval.
Et des limites
Les modèles apportent de l’information supplémentaire, mais aussi du bruit et des erreurs. Plus le modèle est complexe et non linéaire, plus l’incertitude croît, plus la possibilité d’erreur disproportionnée par rapport aux données d’entrée surgit. C’est donc un pêché de naïveté que de croire que l’emploi de modèles sophistiqués peut apporter des avantages. Hormis si l’on est familiarisé avec les biais que les modèles introduisent, aux erreurs qui peuvent être propagées et amplifiées, aux hypothèses qui pourraient être violées et rendre les résultats caducs, je ne crois pas que l’utilisateur occasionnel d’un modèle ait le recul nécessaire face aux résultats de ce modèle. Si l’on prend l’exemple des modèles statistiques du risque financier dans les portefeuilles de titres, l’expérience de la dernière décennie montre les dommages causés par une croyance déraisonnable dans la puissance prédictive des modèles. La morale de cette histoire est que plus un outil est complexe, plus il a le potentiel de fournir de l’information, plus il a aussi la capacité de nous induire lourdement en erreur.
La non-linéarité des modèles est un problème redoutable, source d’erreurs et de comportement chaotique. Dans mon laboratoire de l’EPFL, nous avons illustré récemment que si on prend un fluide newtonien, plus le modèle d’écoulement est sophistiqué, meilleure est sa capacité de prédiction. En revanche, pour des fluides non linéaires (dans notre cas un gel viscoplastique), la précision allait dans le sens inverse du degré de sophistication. On a réalisé des expériences de laboratoire avec des fluides dont les propriétés étaient mesurées indépendamment (pas de biais introduit par un calage). Topographie, conditions initiales et aux limites étaient connues. On cherchait à calculer la vitesse, la hauteur, et la distance d’arrêt. Dans ce contexte très idéalisé des avalanches de fluide, les modèles de Saint-Venant employant les techniques numériques les plus avancées se révélaient bien moins précis que des modèles simples (modèle d’onde cinématique) résolus analytiquement. Cela donne un ordre d’idée des problèmes qui se posent avec des fluides non linéaires.

Avalanche de fluide en laboratoire. Cliché EPFL/LHE. Visualisation par technique de fluorescence laser.
Enfin, l’examen des événements du passé montre qu’il existe des phénomènes anormaux en ce que leurs caractéristiques les rendent très différents de ce qu’on a l’habitude de voir, même parmi les événements exceptionnels. Ces phénomènes sont réellement « extra-ordinaires ». J’ai appelé « horsains » de telles avalanches. Les statisticiens parlent souvent de « outliers », les physiciens de « dragon-roi » (le phénomène qui écrase tous les autres). Donc, même en tentant de reconstituer des événements du passé bien documentés, on peut se trouver en situation d’échec. Il est toujours intéressant de comprendre pourquoi. Dans un article de vulgarisation, j’indiquais les conséquences de tels phénomènes pour les avalanches (2011) :
Le principal intérêt du concept des dragons-rois est de jeter un éclairage nouveau sur les valeurs extrêmes en les distinguant selon leurs origines. Appliqué aux avalanches, ce concept énonce deux choses :
« il existe des avalanches extrêmes, dont les caractéristiques sont, d’un point de vue statistique, en continuité avec les phénomènes ordinaires et rares que connaît le site étudié. Il est raisonnable de penser que la plupart des modèles actuels (statistiques ou dynamiques) peuvent en calculer les caractéristiques à partir de la connaissance de l’activité avalancheuse passée du site ou bien par comparaison avec des sites similaires ;
« il existe des avalanches extrêmes dont les caractéristiques se démarquent nettement des avalanches connues sur le site étudié. Ces avalanches constituent une population à part et il est peu probable que la connaissance de l’historique du site permette de fournir une image correcte de leur dynamique. Il faut au contraire imaginer les scénarios analysant les différentes façons dont des avalanches pourraient s’affranchir des conditions aux limites imposées par le site pour imposer leurs propres conditions. Il ne s’agit pas toutefois de laisser libre cours à des élucubrations. Les processus qui permettent à une avalanche de s’affranchir des « règles du jeu » sont peu nombreux et ne peuvent sans doute pas se produire sur tous les sites. Ce sont de nouvelles règles qui émergent, non l’absence de règles.
Pour terminer, il me faut citer Bruno Salm (2004) :
tous les modèles présentés sont – jusqu’à présent – d’une façon ou d’une autre entachés d’incertitudes. Un accroissement de la complexité des modèles n’implique pas nécessairement une précision plus grande ou une meilleure stratégie de lutte contre les dangers naturels.
C’est une conclusion à méditer…

Détail de l’avalanche des Lanches 25 février 1995 à Peysey-Nancroix. Cliché Gendarmerie de Bourg-Saint-Maurice/Capitaine Margot. L’avalanche est en fait une succession de « langues d’avalanche », qui se sont frayé un chemin à travers ou sur les dépôts des langues précédentes.
Références
Adjel, G., Méthodes statistiques pour la détermination de la distance d’arrêt des avalanches, Université Joseph Fourier, 1996.
Ammann, W.J., Der Lawinenwinter 1999, pp. 588, Eidgenössisches Institut für Schnee- und Lawinenforschung, Davos, 2000.
Ancey, C., and M. Naaim, Modelisation of dense avalanches, in Comptes Rendus de l’Université d’été, edited by G. Brugnot, pp. 173-182., ANENA, Chamonix, 1992.
Ancey, C., Guide Neige et Avalanches : Connaissances, Pratiques, Sécurité, pp. 320, Édisud, Aix-en-Provence, 1996.
Ancey, C., and C. Charlier, Quelques réflexions autour d’une classification des avalanches, Revue de Géographie Alpine, 84, 9-21, 1996.
Ancey, C., Modélisation des avalanches denses, approches théorique et numérique, La Houille Blanche, 5-6, 25-39, 1994.
C. Ancey, M. Meunier, et D. Richard, Inverse problem in avalanche dynamics models, Water Resources Research, 39, 1099, doi:10.1029/2002WR001749, 2003
Ancey, C., Snow avalanches, in Geomorphological Fluid Mechanics: Selected Topics in Geological and Geomorphological Fluid Mechanics, edited by N.J. Balmforth, and A. Provenzale, pp. 319-338, Springer, Berlin, 2001.
Ancey, C., F. Rapin, and M. Meunier, Nivologie pour l’ingénieur, in Géomécanique environnementale : Risques naturels et Patrimoine, edited by B. Schrefler, and P. Delage, pp. 45-68, Hermès, Paris, 2001.
C. Ancey, L’avalanche, l’expert, le modèle, Neige et Avalanches 99 (2002) 29–30.
Ancey, C., C. Gervasoni, and M. Meunier, Computing extreme avalanches, Cold Regions Science and Technology, 39, 161-180, 2004.
Ancey, C., Powder-snow avalanches: approximation as non-Boussinesq clouds with a Richardson-number-dependent entrainment function, Journal of Geophysical Research, 109, F01005, 2004.
Ancey, C., and M. Meunier, Estimating bulk rheological properties of flowing snow avalanches from field data, Journal of Geophysical Research, 109, F01004, 2004.
Ancey, C., S. Cochard, S. Wiederseiner, and M. Rentschler, Front dynamics of supercritical non-Boussinesq gravity currents, Water Resources Research, 42, W08424, 2006.
Ancey, C., Monte Carlo calibration of avalanches described as Coulomb fluid flows, Philosophical Transactions of the Royal Society of London A, 363, 1529-1550, 2005.
Ancey, C., Plasticity and geophysical flows: A review, Journal of Non-Newtonian Fluid Mechanics, 142, 4-35, 2007.
Ancey, C., Gravity Flow on Steep Slope, in Buoyancy Driven Flows, edited by E. Chassignet, C. Cenedese, and J. Verron, Cambridge University Press, New York, 2012.
Ancey, C., N. Andreini, et Epely-Chauvin, Viscoplastic dam break waves: review of simple computational approaches et comparison with experiments, Advances in Water Resources, 48, 79–91, 201.
Andreini, N., Epely-Chauvin, et C. Ancey, Internal dynamics of Newtonian et viscoplastic fluid avalanches down a sloping bed, Physics of Fluids, 24, 053101, 2012.
Ancey, C., Are there ‘dragon-kings’ events (i.e. genuine outliers) among extreme avalanches?, European Physical Journal Special Topics, 205, 117-129, 2012.
Ancey, C., Les avalanches extrêmes sont-elles des horsains ?, Neige & Avalanches, 133, 4-9, 2011.
Ancey, C., Why don’t avalanche-dynamics models of higher complexity necessarily lead to better predictions? International Snow Science Workshop Grenoble – Chamonix Mont-Blanc – 2013, October 2013
Ancey, C., Dynamique des avalanches, Presses Polytechniques et Universitaires Romandes, Lausanne, 2006.
Barbolini, M., U. Gruber, C.J. Keylock, M. Naaim, and F. Savi, Application of statistical and hydraulic-continuum dense-snow avalanche models to five European sites, Cold Regions Science and Technology, 31, 133-149, 2000.
Bartelt, P., J. Glover, T. Feistl, Y. Bühler, and O. Buser, Formation of levees and en-echelon shear planes during snow avalanche run-out, Journal of Glaciology, 58, 980-992, 2012.
Beghin, P., Etude des bouffées bidimensionnelles de densité en écoulement sur pente avec application aux avalanches de neige poudreuse, Institut National Polytechnique de Grenoble, Grenoble, 1979.
Borrel, G., Avalanche risk and French legal building or prevention documents, in Avalanche Dynamics Workshop, edited by H. Gubler, pp. 79-98, SLF, Davos, 1990.
Bovis, M.J., and A.I. Mears, Statistical prediction of snow avalanche runout terrain variables in Colorado, Artic and Alpine Research, 8, 115-120, 1976
Bozhinskiy, N., and K.S. Losev, The fundamentals of avalanche science, EISFL, Davos, 1998.
Bresch, D., E.D. Fern\’andez-Nieto, I.R. Ionescu, and P. Vigneaux, Augmented Lagrangian method and compressible visco-plastic flows: Applications to shallow dense avalanches, in Advances in Mathematical Fluid Mechanics, pp. 57-89, Birkehäuser Verlag, Basel, 2009.
Brugnot, G., and R. Pochat, Numerical simulation study of avalanches, Journal of Glaciology, 27, 77-88, 1981.
Brugnot, G., Modélisation des avalanches, Revue Forestière Française, 34 (5), 131-142, 1982.
Burkard, A., and B. Salm, Die Bestimmung der mittleren Anrissmächtigkeit d° zur Berechnung von Fliesslawinen, Eidgenössisches Institut für Schnee- und Lawinenforschung, Davos, 1992.
Burkard, A., Erfahrung mit der Lawinenzonung in der Schweiz, in Internationales Symposion Interpraevent, pp. 386-407, Interpraevent, Bern, 1992.
Buser, O., and H. Frutiger, Observed maximum run-out distance of snow avalanches and determination of the friction coefficients mu and xi, Journal of Glaciology, 26, 121-130, 1980.
Buser, O., and H. Frutiger, Über maximale Auslaufstrecken von Lawinen und die Bestimmung der Reibungsbeiwerte mu und xi, in Interpraevent Symposion, pp. 125-134, Interpraevent, Graz, 1980.
Carry, C., and R. Pochat, Modélisation d’une avalanche, in 2° rencontre internationale sur la neige et les avalanches, pp. 189-221, ANENA, Grenoble, 1978.
Eckert, N., C.J. Keylock, D. Bertrand, E. Parent, T. Faug, P. Favier, and M. Naaim, Quantitative risk and optimal design approaches in the snow avalanche field: Review and extensions, Cold Regions Science and Technology, 2012. 79-80, 1-19, 2012.
Eckert, N., M. Naaim, and E. Parent, Long-term avalanche hazard assessment with a Bayesian depth-averaged propagation model, Journal of Glaciology, 56, 563-586, 2010.
FAO, Manuel de contrôle des avalanches, Organisation des Nations Unies pour l’agriculture et l’alimentation, division des ressources forestières, Rome, 1978.
Fernandez-Nieto, E.D., P. Noble, and J.-P. Vila, Shallow water equation for non-Newtonian fluids, Journal of Non-Newtonian Fluid Mechanics, 165, 712-732, 2010.
Föhn, P.M.B., Statistische Aspekte bei Lawineneignissen, in International Symposium Interpraevent, pp. 293-304, Innsbruck, 1975.
Föhn, P.M.B., and R. Meister, Determination of avalanche magnitude and frequency by direct observations and/or with the aid of indirect snowcover data, in IUFRO/FAO Colloquium on research on small torrential watersheds (incl. avalanches), pp. 207-227, Forstlichen Bunderverschusanstalt, Wien, Grenoble, 1981.
Grigorian, S.S., Mechanics of snow avalanches, in Mécanique de la neige, pp. 355-368, International Association of Hydrological Sciences, Grindelwald, 1974.
Heimgartner, M., On the flow of avalanche snow, Journal of Glaciology, 19, 357-363, 1977.
Hopfinger, E.J., and J.-C. Tochon-Danguy, A model study of powder-snow avalanches, Journal of Glaciology, 81, 343-356, 1977.
Keiler, M., R.J. Sailer, P., C. Weber, M. Fuchs, A. Zischg, and S. Sauermoser, Avalanche risk assessment – a multi-temporal approach, results from Galtür, Austria, Natural Hazards and Earth System Sciences, 6, 637-651, 2006.
LaChapelle, E.R., and T.E. Lang, A comparison of observed and calculated avalanche velocities, Journal of Glaciology, 309–314, 1980.
Lagotala, H., Étude de l’avalanche des Pélerins (Chamonix), Société Générale d’Imprimerie, Genève, 1927.
Lied, K., and R. Toppe, Calculation of maximum snow avalanche runout distance based on topographic parameters identified by digital terrain models, Annals of Glaciology, 13, 164-169, 1989.
Martinet, G., Contribution à la modélisation numérique des avalanches de neige dense et aux laves torrentielles, University Joseph Fourier, Grenoble, 1992.
Mears, A.I., Snow-avalanche hazard analysis for land-use planning and Engineering, Colorado Geological Survey, Denver, 1992.
Meunier, M., C. Ancey, et D. Richard, L’approche conceptuelle pour l’étude des avalanches, Cemagref éditions, Anthony, 2004.
Meunier, M., and C. Ancey, Towards a conceptual approach to predetermining long-return-period avalanche run-out distances, Journal of Glaciology, 50, 268-278, 2004.
Meunier, M., C. Ancey, and J.-M. Taillandier, Fitting avalanche-dynamics models with documented events from the Col du Lautaret site (France) using the conceptual approach, Cold Regions Science and Technology, 39, 55-66, 2004.
Mougin, P., Les avalanches en Savoie, 175-317 pp., Ministère de l’Agriculture, Direction Générale des Eaux et Forêts, Service des Grandes Forces Hydrauliques, Paris, 1922.
Naaim, M., Numerical model of powder snow avalanche. Theoretical analysis and application, in Les apports de la recherche scientifique à la securité neige, glace et avalanche, coord. par ANENA, pp. 31-36, Cemagref, Chamonix, 1995.
Perla, R.I., T.T. Cheng, and D.M. McClung, A two-parameter model of snow-avalanche motion, Journal of Glaciology, 26, 197-202, 1980.
Rapin, F., The French theory for snow avalanches with aerosol, in Université européenne d’été sur les risques naturels, edited by G. Brugnot, Cemagref, Chamonix, 1992.
Salm, B., Contribution to avalanche dynamics, in Scientific Aspects of Snow and Ice Avalanche, pp. 199-214, IAHS Press, Wallingford, Oxfordshire, UK, Davos, 1966.
Salm, B., A. Burkard, and H. Gubler, Berechnung von Fliesslawinen, eine Anleitung für Praktiker mit Beispielen, Eidgenössisches Institut für Schnee- und Lawinenforschung (Davos), 1990.
Salm, B., A short and personal history of snow avalanche dynamics, Cold Regions Science and Technology, 39, 83-92, 2004.
Sornette, D., et G. Ouillon, Dragon-kings: Mechanisms, statistical methods et empirical evidence, European Physical Journal Special Topics, 205, 1-26, 2012.
Tochon-Danguy, J.-C., Etude des courants de gravité sur forte pente avec application aux avalanches poudreuses, Institut National Polytechnique de Grenoble, Grenoble, 1977.
Turnbull, B., J. McElwaine, and C. Ancey, The Kulikovskiy–Sveshnikova–Beghin model of powder snow avalanches: Development and application, Journal of Geophysical Research, 112, F01004, 2007.
Vila, J.P., Sur la théorie et l’approximation numérique des problèmes hyperboliques non-linéaires, application aux équations de Saint-Venant et à la modélisation des avalanches denses, Ph.D. thesis thesis, Paris VI, 1986.
Voellmy, A., Über die Zerstörungskraft von Lawinen, Schweizerische Bauzeitung, 73, 159–162, 212–217, 246–249, 280–285., 1955.





